Atividade sobre Função Exponencial - Ensino Médio

➡️ Apresentamos uma excelente Atividade de Matemática sobre Função Exponencial para o Ensino médio. Conheça, baixe e aplique em sala de aula!

Download e planejamento do conteúdo disponíveis no final da publicação

1. Um medicamento mantém apenas 80% da sua quantidade no corpo após cada hora. Se um paciente recebeu 50 mg, qual função representa a quantidade de medicamento após t horas?
a) f(t) = 50 . 0,8^t
b) f(t) = 50 – 0,8^t
c) f(t) = 50 – 1,8^t
d) f(t) = 50 . 1,8^t
e) f(t) = 50 . t^0,8

2. O valor de um equipamento desvaloriza 5% ao ano. Se o valor inicial é de R$ 2.000, qual função representa o valor após t anos?
a) f(t) = 2000 . (0,95)^t
b) f(t) = 2000 – 0,95t
c) f(t) = 2000 – (1,05)^t
d) f(t) = 2000 . (1,05)^t
e) f(t) = 2000 . t^0,95

3. Observe o gráfico de uma função exponencial.

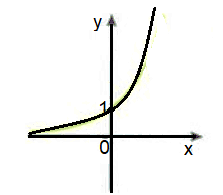
Qual das funções a seguir corresponde ao gráfico apresentado?
a) f(x) = 3x²
b) f(x) = 2x 
c) f(x) = ( )^x
d) f(x) = 3^-x
e) f(x) = 2^x

4. Observe a função exponencial que o professor de Lucas escreveu no quadro.

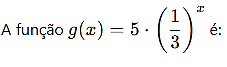
Esta função pode ser classificada como
a) crescente, pois a base é maior que 1.
b) decrescente, pois a base está entre 0 e 1.
c) crescente, pois o coeficiente é positivo.
d) constante, pois a base é fracionária.
e) constante, pois a base está entre 0 e 1.

5. Durante uma investigação científica no laboratório da escola, os alunos observaram uma colônia de bactérias colocada em uma placa de cultivo. Descobriu-se que essa colônia dobra sua quantidade a cada hora. No início da observação, havia 200 bactérias. Qual função representa o número de bactérias após t horas?
a) f(t) = 200 . 2^t
b) f(t) = 200 . t²
c) f(t) = 200 . (1,02)^t
d) f(t) = 200 + 2t
e) f(t) = 200 + ( )^t

6. Considere a função f(x) =  3 ⋅ 2^x .Qual é o valor de f(3)?
a) 6                      
b) 9                     
c) 18               
d) 24                   
e) 32

7. Laís resolveu fazer um investimento e aplicou um capital de R$ 1 000,00 a uma taxa de 5% ao mês no regime de juros compostos. O valor V acumulado nesta aplicação após x meses pode ser calculado pela função
a) V(x) = 1000 ⋅ (0,05)^x.   
b) V(x) = 1000 ⋅ (1,05)^x.   
c) V(x) = 1000 + (0,05)^x.   
d) V(x) = 1000 + (1,05)^x.   
e) V(x) = 1000 ⋅ (1,05)^x.   

8. Considere a função exponencial abaixo. 

f(x) = ( )^x

Qual é o valor de f(2)?
a) 13                     
b) 16                  
c) 19                      
d) 3²                       
e) 3³

9. Em um experimento de Física, a intensidade de uma radiação cresce de acordo com a função I(t) = 2^t em que I(t) é a intensidade medida em unidades arbitrárias e t é o tempo em segundos. Qual é o valor da intensidade após 5 segundos?
a) 6          
b) 8                  
c) 10            
d) 16        
e) 32

10. Em uma estação de pesquisa ambiental, os técnicos monitoram a população de uma espécie de inseto que se reproduz rapidamente. Sabe-se que essa população cresce 8% ao dia. No início do estudo, havia 500 insetos na área observada.  A função que representa a quantidade de insetos após t dias é:

P(t) = 500 ⋅ 1,08^t

Qual é a quantidade aproximada de insetos após 3 dias?
a) 500                
b) 540               
c) 630                 
d) 680            
e) 734

---

+ Conteúdos de Funções

Matemática 8º e 9º ano

Exercícios de Função Afim – Com Gabarito

Matemática 8º e 9º ano

Exercícios – Atividade sobre Função Quadrática – 8° ano – 9° ano – com gabarito

---

+ Conteúdos de Ensino Médio

Confira nossa página repleta de conteúdos semelhantes, especialmente desenvolvidos para esse público escolar. Materiais pedagógicos de alta qualidade, cuidadosamente preparados pelos produtores do Tudo Sala de Aula. Clique agora e escolha o tema da aula!

Acesse outros exercícios

Planejamento para o professor

Objeto do conhecimento: Função exponencial.

Objetivo da Aula: Analisar e estabelecer relações entre as representações algébrica e gráfica de funções exponenciais; Resolver problemas envolvendo função exponencial.

Habilidade da BNCC: (EM13MAT304) Resolver e elaborar problemas que envolvam funções exponenciais, interpretando a variação das grandezas em contextos como matemática financeira e outros.

BAIXAR EXERCÍCIO

Por favor, não compartilhe o PDF!

Gostou? Deixe um comentário!😍

Por Eleí dos Santos
Licenciada em Matemática, especialista em Didática da Matemática, Psicopedagogia e Educação Especial.

O conteúdo foi revisado e certificado pela equipe de Redação do Tudo Sala de Aula.