➡️ Preparamos uma excelente Atividade de Matemática com Problemas sobre a Independência do Brasil, direcionada aos estudantes do 8º e 9º ano. A proposta integra conteúdos matemáticos variados com fatos históricos, tornando o aprendizado mais dinâmico e desafiador, estimulando o raciocínio lógico, a resolução de problemas e a contextualização histórica. Conheça, baixe e aplique em sala de aula!
Download e planejamento do conteúdo disponíveis no final da publicação

1. Para o desfile de 7 de setembro de um município, uma escola levou 800 alunos para a avenida. Destes, 35% participaram tocando na fanfarra. Quantos alunos tocaram na fanfarra?
a) 240
b) 260
c) 280
d) 300
2. No desfile, um grupo de alunos carregou uma bandeira do Brasil em formato retangular de 4 m de comprimento por 2,5 m de largura. Qual é a área total dessa bandeira?
a) 7 m².
b) 8 m².
c) 9 m².
d) 10 m².
3. Em uma escola, será sorteado um aluno para representar um dos soldados da Independência no dia 7 de setembro. No total, 20 alunos se inscreveram, sendo 8 deles do ensino fundamental I e 12 do fundamental II. Qual a probabilidade de que, sendo escolhido ao acaso, o sorteado seja do ensino fundamental I?
a) 20%.
b) 28%.
c) 40%.
d) 60%.
4. Na praça central de uma localidade, foram utilizadas bandeirinhas no formato de triângulo isósceles para a decoração do desfile da Independência. As medidas da bandeira estão indicadas na figura.
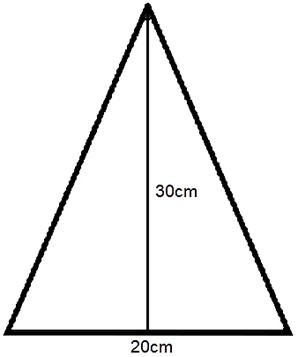
Qual a área de cada bandeirinha?
a) 120 cm².
b) 300 cm².
c) 450 cm².
d) 600 cm².
5. Numa turma que desfilou no 7 de setembro, os alunos marcharam em 5 filas com os seguintes números de integrantes: 12, 15, 18, 15 e 20. Considerando esses valores, qual a média de alunos por fila?
a) 14
b) 15
c) 16
d) 17
6. Em uma sacola, há 10 bandeirinhas verdes, 6 amarelas e 4 azuis. Se um aluno pegar uma bandeirinha ao acaso, qual é a probabilidade de ela ser amarela?
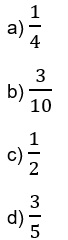
7. Um grupo de jovens da Secretaria da Cultura confeccionou um grande tambor, no formato de cilindro, para representar a fanfarra no desfile da Independência. O tambor possui raio da base igual a 15 cm e altura 30 cm, conforme representado na figura abaixo.
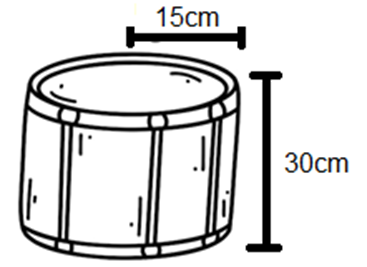
Qual o volume desse tambor, em função de π?
a) 6.750π cm³.
b) 7.500π cm³.
c) 10.125π cm³.
d) 13.500π cm³.
8. No coral cívico da escola de Raphaela, dos alunos cantaram o Hino Nacional e o restante cantou o Hino da Independência. Se havia 60 alunos, quantos cantaram o Hino da Independência?
a) 36
b) 40
c) 42
d) 50
9. Uma bandeira do Brasil tem dimensões de 7 cm de altura por 10 cm de comprimento. Se essa bandeira for ampliada para que o comprimento passe a medir 120 cm, mantendo-se a mesma proporção, qual será a sua altura?
a) 72 cm.
b) 80 cm.
c) 84 cm.
d) 90 cm.
10. O lucro (L), em reais, de um vendedor ambulante com a venda de bandeirinhas do Brasil, é dado pela função: L(x) = 2x + 50, onde x é o número de bandeirinhas vendidas. Qual será o lucro desse vendedor se ele vender 25 bandeirinhas?
a) R$ 90,00
b) R$ 100,00
c) R$ 110,00
d) R$ 120,00
+ Conteúdos de Matemática para o 8º e 9º ano
Confira nossa página repleta de conteúdos semelhantes, especialmente desenvolvidos para esse público escolar. Materiais pedagógicos de alta qualidade, cuidadosamente preparados pelos produtores do Tudo Sala de Aula. Clique agora e escolha o tema da aula!
Planejamento para o professor
Objeto do conhecimento: Porcentagem, Área de figuras planas, Probabilidade, Função do 1º grau, Média Aritmética, Frações, Semelhança de figuras e Volume.
Objetivo da Aula: Trabalhar os conteúdos de Porcentagem, Área de figuras planas, Probabilidade, Função do 1º grau, Média Aritmética, Frações, Semelhança de figuras e Volume, por meio de atividades lúdicas e problemas matemáticos relacionados à Independência do Brasil, estimulando o raciocínio lógico, a aplicação prática dos conceitos e a contextualização histórica.
Habilidade do SAEB: 9E1.5 – Calcular os valores de medidas de tendência central de uma pesquisa estatística (média aritmética simples, moda ou mediana). 9E2.4 – Resolver problemas que envolvam a probabilidade de ocorrência de um resultado em eventos aleatórios equiprováveis independentes ou dependentes. 9M2.4 – Resolver problemas que envolvam volume de prismas retos ou cilindros retos. 9A2.5 – Resolver problemas que envolvam função afim. 9N2.1 – Resolver problemas de adição, subtração, multiplicação, divisão, potenciação ou radiciação envolvendo números reais, inclusive notação científica. 9N2.3 – Resolver problemas que envolvam porcentagens, incluindo os que lidam com acréscimos e decréscimos simples, aplicação de percentuais sucessivos e determinação das taxas percentuais. 9G2.5 – Resolver problemas que envolvam polígonos semelhantes.
Por favor, não compartilhe o PDF!
Reiteramos que todo o conteúdo do site Tudo Sala de Aula é original, produzido por equipe própria. Portanto, este material, assim como os demais, não pode ser publicado em sites pessoais ou copiado para a criação de apostilas para venda. Pirataria é crime! Estamos de olho! (Lei 9.610/98)
Gostou? Deixe um comentário!😍

Por Eleí dos Santos
Licenciada em Matemática, especialista em Didática da Matemática, Psicopedagogia e Educação Especial.
O conteúdo foi revisado e certificado pela equipe de Redação do Tudo Sala de Aula.








