📝 Excelente Atividade de Matemática sobre Volume de Blocos Retangulares para os estudantes do 7º e 8º ano. Através do estudo do volume, os alunos aprendem a calcular a capacidade de sólidos retangulares, interpretando dados e utilizando unidades de medida com precisão. Conheça, baixe e aplique esse material feito pela equipe do Tudo Sala de Aula!
Download e planejamento do conteúdo disponíveis no final da publicação
🔎 Saiba mais:
O volume de um bloco retangular indica quanto espaço ele ocupa no interior. Para calcular esse volume, usamos a fórmula:
Volume = comprimento × largura × altura
Lembrando que todas as medidas precisam estar na mesma unidade. O resultado será expresso em unidades cúbicas, como cm³ (centímetros cúbicos) ou m³ (metros cúbicos). Para transformar esse volume em litros, usamos a equivalência:
1 litro = 1.000 cm³
1000 litros = 1 m³
📚 Atividades
1. Luiza é dona de uma loja de plásticos e comercializa três tipos diferentes de potes. Veja os modelos a seguir.
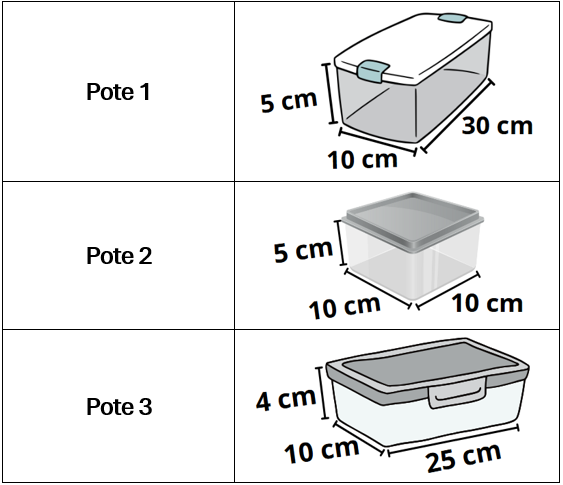
Agora, calcule a capacidade de cada um desses potes.
2. Carlos comprou uma caixa retangular para guardar brinquedos. A caixa tem 50 cm de comprimento, 40 cm de largura e 25 cm de altura. Qual é o volume da caixa de Carlos, em cm³?
3. Lorena comprou um aquário para criar peixinhos e colocou água até a metade do aquário.
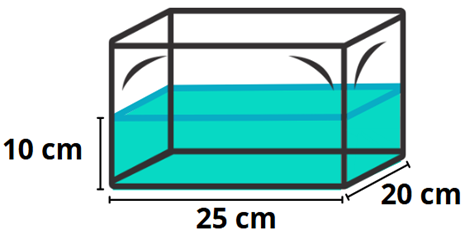
Qual a capacidade total desse aquário, em litros?
a) 5 litros.
b) 10 litros.
c) 50 litros.
d) 100 litros.
4. Ronaldo comprou uma caixa de isopor para colocar gelo e manter os refrigerantes gelados na festa de aniversário de sua filha. Observe, a seguir, a caixa que ele adquiriu.
a) Qual é a capacidade total dessa caixa, em centímetros cúbicos?
b) E qual é essa capacidade, em litros?
5. Henrique é dono de uma indústria de laticínios e comprou um novo tanque de resfriamento para armazenar leite. Veja a seguir.
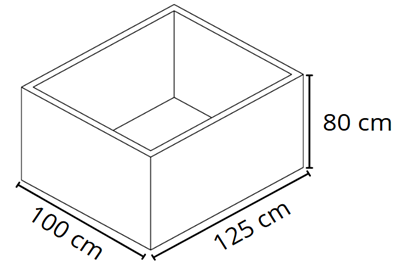
Quantos litros de leite esse tanque pode armazenar?
a) 10 000 L.
b) 1 000 L.
c) 100 L.
d) 10 L.
6. Augusto trabalha com a venda de relógios no atacado e recebeu um novo pedido. Cada relógio acompanha uma caixinha individual, como mostra a imagem a seguir.
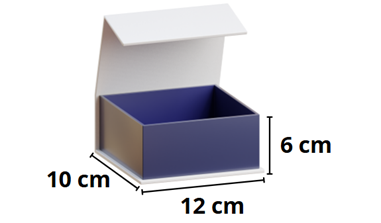
Para o transporte, ele organizará as caixinhas dentro de uma caixa maior, cujas dimensões estão indicadas abaixo.
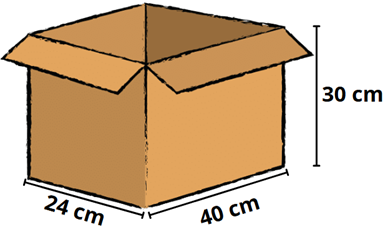
Quantas caixinhas de relógio podem ser acomodadas dentro da caixa maior, sem deixar espaços vazios?
a) 28
b) 35
c) 40
d) 72
7. Observe a piscina a seguir.
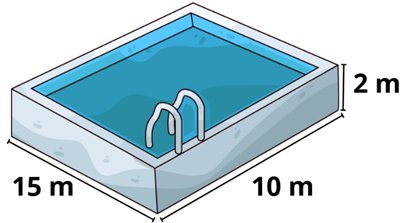
Qual a capacidade dessa piscina?
a) 300 litros.
b) 3 000 litros.
c) 30 000 litros.
d) 300 000 litros.
8. João comprou um recipiente retangular de Marmitex para usar no seu novo trabalho. Suas medidas são: 18 cm de comprimento, 12 cm de largura e 8 cm de altura. Qual é a capacidade desse recipiente?
9. Thiago ganhou uma caixa com blocos de montar e derrubou todos de uma vez. Depois de brincar, ele guardou apenas algumas peças, como mostrado a seguir.
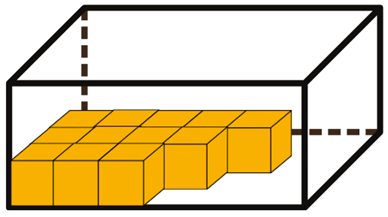
Sabendo que cada bloquinho possui 1 cm³ de volume e que o volume total da caixa é de 36 cm³, quantos bloquinhos ainda faltam ser colocados na caixa?
10. Nelson trabalha em uma construção e precisa alugar uma caçamba para transportar entulho. A caçamba tem formato retangular, com 3 metros de comprimento, 2 metros de largura e 1,2 metro de altura. Qual é a capacidade total dessa caçamba?
a) 7,2 m³.
b) 72 m³.
c) 720 m³.
d) 7 200 m³.
+ Conteúdos de Matemática para o 6º e 7º ano
Confira nossa página repleta de conteúdos semelhantes, especialmente desenvolvidos para esse público escolar. Materiais pedagógicos de alta qualidade, cuidadosamente preparados pelos produtores do Tudo Sala de Aula. Clique agora e escolha o tema da aula!
Planejamento para o professor
Objeto do conhecimento: Volume de blocos retangulares.
Objetivo da Aula: Calcular o volume de blocos retangulares usando a fórmula e entender a conversão de unidades de volume.
Habilidade da BNCC: (EF07MA30) Resolver e elaborar problemas de cálculo de medida do volume de blocos retangulares, envolvendo as unidades usuais (metro cúbico, decímetro cúbico e centímetro cúbico).
BAIXAR EXERCÍCIOPor favor, não compartilhe o PDF!
Reiteramos que todo o conteúdo do site Tudo Sala de Aula é original, produzido por equipe própria. Portanto, este material, assim como os demais, não pode ser publicado em sites pessoais ou copiado para a criação de apostilas para venda. Pirataria é crime! Estamos de olho! (Lei 9.610/98)
Gostou? Deixe um comentário!😍
Por Geiciane Santos
Licenciada em Matemática, Bacharel em Administração e pós-graduada em Ensino de Matemática.
O conteúdo foi revisado e certificado pela equipe de Redação do Tudo Sala de Aula.
