Atividade de Matemática sobre as Relações Métricas no Triângulo Retângulo para os estudantes do 8º e 9º ano. As relações métricas no triângulo retângulo permitem calcular medidas de segmentos e ângulos por meio de teoremas e propriedades matemáticas específicas. Ao trabalhar com essa atividade, os alunos desenvolvem habilidades de raciocínio lógico, cálculo e aplicação de fórmulas matemáticas. Baixe gratuitamente e aplique com seus alunos!
Planejamento para o professor
Objeto do conhecimento: Relações métricas no Triângulo Retângulo.
Objetivo da Aula: Compreender as relações métricas no triângulo retângulo, aplicando o Teorema de Pitágoras e as razões trigonométricas para resolver problemas.
Habilidade da BNCC: (EF09MA13) Demonstrar relações métricas do triângulo retângulo, entre elas o teorema de Pitágoras, utilizando, inclusive, a semelhança de triângulos.
Download do conteúdo disponível no final da publicação
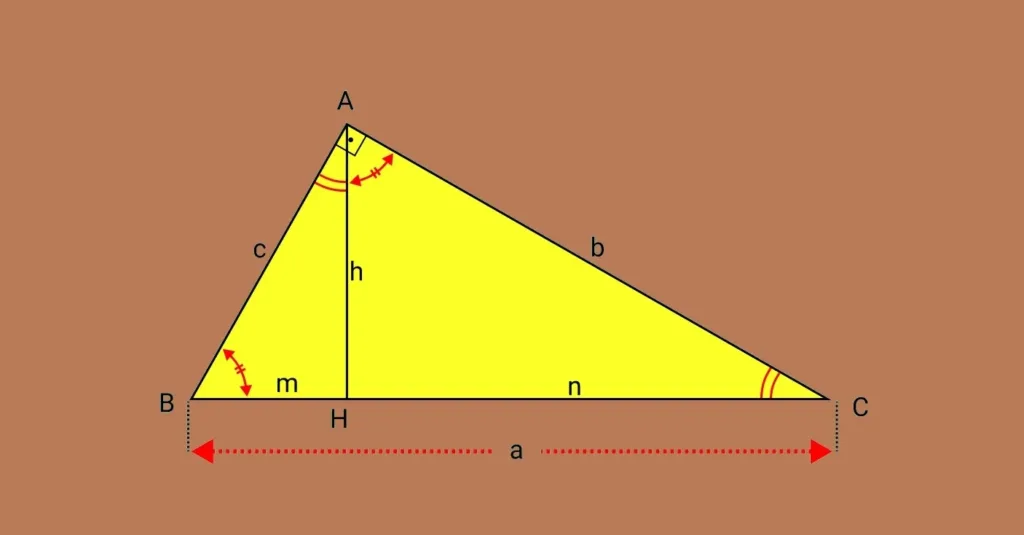
1. Para finalizar a instalação de energia elétrica, Joaquim precisa medir a altura da tesoura do teto da sua área de serviço, representada pelo triângulo retângulo a seguir.
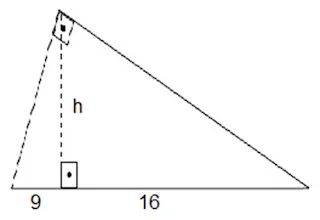
Considerando as medidas que dispõe, que relação métrica ele deve aplicar?
a) a.h = b.c
b) h2 = m.n
c) a2 = b2 + c2
d) c2 = a.m
2. Aplicando corretamente a relação métrica e efetuando os cálculos na questão anterior, qual o resultado encontrado?
a) 9
b) 10
c) 12
d) 16
3. Em um triângulo retângulo, a hipotenusa e os catetos medem, respectivamente, 15, 12 e 9 cm. Desse modo, a altura relativa à hipotenusa, vale:
a) 7,2
b) 8
c) 8,5
d) 12
4. Tiro ao alvo é o nome do jogo inventado por Jobson que consiste em arremessar uma bola a uma distância de 6 metros de uma parede, de modo que, percorrendo a diagonal, a bola atinja o ponto mais alto da parede e retorne ao chão, conforme desenho.
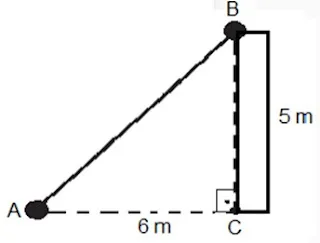
Considerando que Jobson jogou a bola do ponto indicado pela letra A e ela atingiu a altura máxima, no ponto B, descendo encostada na parede até retornar ao solo, a distância total percorrida pela bola, nessa jogada, foi de
a) 7,8 m aproximadamente.
b) 8 m aproximadamente.
c) 12,8 m aproximadamente.
d) 16 m aproximadamente.
5. O Auditório Ibirapuera, em São Paulo, tem laterais com formato de triângulo retângulo, conforme a imagem.

Considerando que a lateral direita tem 28 metros de altura e 15 metros de comprimento, a medida da hipotenusa, em metros, equivale a aproximadamente
a) 28 m.
b) 32 m.
c) 35 m.
d) 44 m.
6. Aplicando as relações métricas no triângulo retângulo a seguir, ajude o arquiteto calcular as medidas indicadas pelas letras x e h na tesoura, sabendo que as projeções dos catetos sobre a hipotenusa medem 4 e 9.

Os valores encontrados, em valores aproximados, foram
a) x = 4 e h = 6
b) x = 4 e h = 9
c) x = 5,6 e h = 6
d) x = 7,2 e h = 6
7. A figura a seguir representa uma rampa que dá acesso a uma sala, em posição paralela às paredes laterais. Com base nas medidas indicadas na figura, determine a distância percorrida por uma pessoa que sair do ponto A ao ponto E?
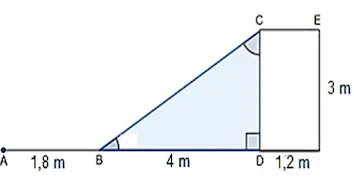
a) 5
b) 6,8
c) 7,2
d) 8,0
8. No Brasil, a Lei de Acessibilidade exige, em todos os estabelecimentos, a construção de rampas de acesso. A sala de recepção de uma casa de apoio tinha seu acesso dificultado pela altura do seu piso em relação ao solo e, para garantir a acessibilidade, a Prefeitura mandou construir uma rampa, com dimensões dadas na figura a seguir.

Qual o comprimento da rampa?
a) 7m
b) 8m
c) 9m
d) 11m
9. Jorge dividiu um terreno plano horizontal para seus dois filhos usando o modelo inspirado pelos egípcios. Fixou duas estacas nos pontos A e B, ligando-os com uma corda. Em seguida, esticou mais duas cordas do ponto B aos pontos C e D, demarcando o terreno de cada filho, conforme a imagem.
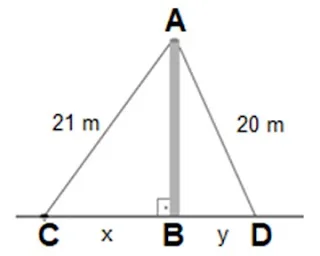
Com base nas dimensões estabelecidas, determine a soma das medidas x e y do terreno.
a) 21
b) 28
c) 29
d) 41
10. Dado um triângulo retângulo onde as projeções dos catetos sobre a hipotenusa medem 4 e 21 centímetros, a medida dos catetos são iguais a
a) 10 e 25
b) 10 e 5√21
c) 21 e 5√21
d) 21 e 25
+ Conteúdos de Matemática para o 8° e 9° ano
Confira nossa página repleta de conteúdos semelhantes, especialmente desenvolvidos para esse público escolar. Materiais pedagógicos de alta qualidade, cuidadosamente preparados pelos produtores do Tudo Sala de Aula. Clique agora e escolha o tema da aula!
Por favor, não compartilhe o PDF!
Reiteramos que todo o conteúdo do site Tudo Sala de Aula é original, produzido por equipe própria. Portanto, este material, assim como os demais, não pode ser publicado em sites pessoais ou copiado para a criação de apostilas para venda. Pirataria é crime! Estamos de olho! (Lei 9.610/98)
Feito por Eleí dos Santos
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Aenean fermentum quis odio a mattis. Pellentesque eu sapien eget lectus lobortis laoreet.
Revisado por Redação Tudo Sala de aula






