Questões de Concurso de Matemática sobre Função do 2º Grau com Gabarito

1. (INSTITUTO EXCELÊNCIA) A equação do segundo grau recebe esse nome pelo fato de o grau da função (expoente de maior valor) ser igual a dois. Considere a seguinte equação e o seu gráfico plotado:

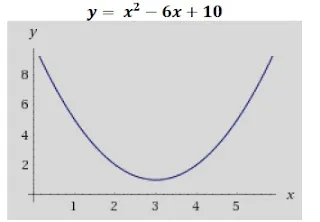
Avalie agora as seguintes proposições:

I - A função apresenta duas raízes reais.

II - O ponto de mínimo da função é (3, 1).

III - A função não apresenta valores negativos (y < 0) para todo o domínio de x.

É/são CORRETA(S) somente a(s) proposição(ões):

a) I.

b) II.

c) III.

d) II e III.

e) I e II.

 

2. (GUALIMP) Marque a alternativa abaixo que apresenta a expressão algébrica da função do 2º grau que passa pelos três pontos: A(2,9); B(1,5); C(0,7).

a) f(x) = 2x² – x + 7.

b) f(x) = 3x² – 5x + 7.

c) f(x) = x² – 3x + 7.

d) f(x) = x² – x + 7

.

3. (GUALIMP) Um canhão de guerra lançou uma bola para frente, onde a bola fez uma trajetória parabólica descrita pela função S(t) = 30t - t2, onde S(t) representa a altura atingida pela bola, em metros, e t representa o tempo, em segundos. Qual foi a altura máxima atingida pela bola?

a) 30 m.

b) 125 m.

c) 225 m.

d) 300 m.

 

4. (FUNDATEC) Em um teste de artilharia do Exército Nacional, foram usadas novas armas cuja potência de alcance máximo vertical é dado pelo ponto máximo da seguinte função de segundo grau: -x² + 4x +10=0. A altura máxima verificada no teste, em km, foi de:

a) 14.

b) 28.

c) 42.

d) 56.

e) 70.

 

5. (FUMARC) Se a abscissa do vértice da parábola que representa o gráfico da função f(x) = 2x² −(m − 3) x + 5 é igual a 1 e m é um número real positivo, então é CORRETO afirmar que a ordenada do vértice e o valor m são, respectivamente, iguais a:

a) 3 e 4

b) 3 e 7

c) 4 e 3

d) 7 e 3

 

6. (CEPROS) A concentração C, em função do tempo t, de determinado medicamento na corrente sanguínea de um paciente, é dada por C(t) = -0,04t² + 6t + 20, em que t = 0 é o instante em que o paciente ingere a primeira dose do medicamento. O tempo t é medido em horas, e a concentração C(t) em partes por milhão. Se o paciente ingeriu a primeira dose às 8h00, a que horas a concentração atingirá 76 partes por milhão, pela primeira vez? Abaixo, temos uma ilustração do gráfico de C em termos de t.

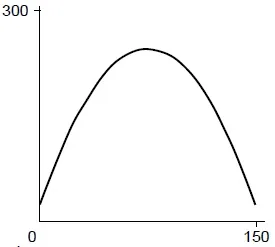
a) ás 15h00

b) ás 16h00

c) ás 17h00

d) ás 18h00

e) ás 19h00

 

6. (COTEC) Encontre o domínio da função f(x) = √3x - 1.

a) D = x ∈ R / x ≥ 1.

b) D = x ∈ R / x ≥ 2.

c) D = x ∈ R / x ≥ 0.

d) D = x ∈ R / x ≥ 4.

e) D = R

 

7. Sendo f(x) = a^x , a > 0 e a ≠ 1, onde m e n números reais quaisquer, analise e classifique os itens.

I - f( m + n) = f(m) + f(n)

II - f( m + n) = f(m) . f(n)

III - f(m . n) = f(m) . f(n) IV - f(m . n) =(f(m))ⁿ V - f (m - n) = f(m) : f(n)

Assinale a alternativa que contém as afirmativas CORRETAS:

a) II, III e IV, apenas.

b) II, IV e V, apenas.

c) III, IV e V, apenas.

d) I, II e IV, apenas.

e) I, III e IV, apenas.

 

8. (IDCAP) Considere a seguinte função:

f(x) = 3x² – 5x + 2.

I- Trata-se de uma função do 2º grau;

II- Tem-se que f(0) = 3;

III- Se f(x) = 0, a função não possui raízes reais.

Dos itens acima,

a) Apenas o item I está correto.

b) Apenas o item II está correto.

c) Apenas os itens I e II estão corretos

d) Apenas os itens I e III estão corretos

e) Todos os itens estão corretos.

 

9. (FUNDATEC) Dada a função f(x) = −2x² − 11x + 6 é INCORRETO afirmar que:

a) Possui duas raízes distintas.

b) Seu gráfico possui valor máximo.

c) A concavidade é voltada para baixo.

d) As raízes são inteiras.

e) A soma das raízes é um número negativo.

 

10. (INSTITUTO EXCELÊNCIA) Dada uma função quadrática f:R → R definida por f(g) = g² +3g − 6, o valor mínimo da função é:

a) 8,25

b) -8,25

c) 16,5

d) -16,5

e) Nenhuma das alternativas.

Voltar ao MENU de Matemática

GABARITO

1D / 2B / 3C / 4A /5B / 6C / 7B / 8A / 9D / 10B

Deixe um comentário mais abaixo avaliando esta atividade, é só rolar a página! Ficaremos felizes com seu comentário.